
문제
방향성이 없는 그래프가 주어진다. 세준이는 1번 정점에서 N번 정점으로 최단 거리로 이동하려고 한다. 또한 세준이는 두 가지 조건을 만족하면서 이동하는 특정한 최단 경로를 구하고 싶은데, 그것은 바로 임의로 주어진 두 정점은 반드시 통과해야 한다는 것이다.
세준이는 한번 이동했던 정점은 물론, 한번 이동했던 간선도 다시 이동할 수 있다. 하지만 반드시 최단 경로로 이동해야 한다는 사실에 주의하라. 1번 정점에서 N번 정점으로 이동할 때, 주어진 두 정점을 반드시 거치면서 최단 경로로 이동하는 프로그램을 작성하시오.
입력
첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000) 둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데, a번 정점에서 b번 정점까지 양방향 길이 존재하며, 그 거리가 c라는 뜻이다. (1 ≤ c ≤ 1,000) 다음 줄에는 반드시 거쳐야 하는 두 개의 서로 다른 정점 번호 v1과 v2가 주어진다. (v1 ≠ v2, v1 ≠ N, v2 ≠ 1) 임의의 두 정점 u와 v사이에는 간선이 최대 1개 존재한다.
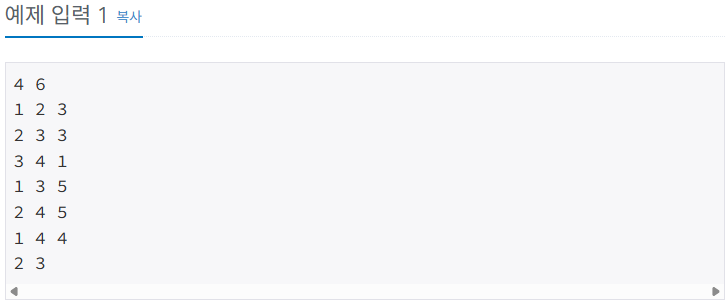
출력
첫째 줄에 두 개의 정점을 지나는 최단 경로의 길이를 출력한다. 그러한 경로가 없을 때에는 -1을 출력한다.

문제풀이
알고리즘 선택 - 다익스트라(dijkstra)
그래프가 주어졌을 때, 반드시 거쳐야 하는 두 정점 v1, v2를 지나는 최단 경로의 길이를 구하는 문제이다. 단방향이 아닌 양방향 그래프이며, 간선에 가중치가 존재한다. 시작점은 항상 1번 정점, 도착점은 N번 정점, 또한 다음 두 경로 중 최단 경로를 계산해야 한다.
- 1 → v1 → v2 → N
- 1 → v2 → v1 → N
두 경우 각각에 대해 다익스트라 알고리즘을 세 번씩 돌려 최단 경로 길이를 계산한 뒤, 더 짧은 쪽을 선택할 것이다.
자료구조 정의
static class Edge implements Comparable<Edge> {
int u;
int cost;
Edge(int u, int cost) {
this.u = u;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return cost - o.cost;
}
}
static int N, E;
static int v1, v2;
static List<List<Edge>> graph;
static int[] dist;
static boolean[] check;
static final int INF = 2_000_000;다익스트라 알고리즘 수행 시 PQ를 활용한 최적화에 정렬 규칙이 필요하므로 Comparable의 구현체로 Edge 클래스를 정의한다. 이 Edge 클래스는 다익스트라 우선순위 큐에 사용될 엣지 정보를 담는다. 이 클래스를 활용하여 인접 리스트로 그래프를 표현하는 graph, 시작점에서의 최단 거리 저장 배열 dist, 방문 여부를 확인하는 배열 check를 선언한다.
풀이 구현
public static int dijkstra(int start, int end) {
Arrays.fill(dist, INF);
Arrays.fill(check, false);
PriorityQueue<Edge> pq = new PriorityQueue<>();
boolean[] check = new boolean[N + 1];
pq.offer(new Edge(start, 0));
dist[start] = 0;
while (!pq.isEmpty()) {
Edge curEdge = pq.poll();
int cur = curEdge.u;
if (!check[cur]) {
check[cur] = true;
for (Edge edge : graph.get(cur)) {
if (!check[edge.u] && dist[edge.u] > dist[cur] + edge.cost) {
dist[edge.u] = dist[cur] + edge.cost;
pq.add(new Edge(edge.u, dist[edge.u]));
}
}
}
}
return dist[end];
}가장 기본적인 다익스트라 알고리즘 구현을 따르기 때문에 설명은 생략한다.
전체코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Boj1504 {
static class Edge implements Comparable<Edge> {
int u;
int cost;
Edge(int u, int cost) {
this.u = u;
this.cost = cost;
}
@Override
public int compareTo(Edge o) {
return cost - o.cost;
}
}
static int N, E;
static int v1, v2;
static List<List<Edge>> graph;
static int[] dist;
static boolean[] check;
static final int INF = 2_000_000;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
graph = new ArrayList<>();
dist = new int[N + 1];
check = new boolean[N + 1];
Arrays.fill(dist, INF);
for (int i = 0; i <= N; i++) {
graph.add(new ArrayList<>());
}
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken());
int v = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
graph.get(u).add(new Edge(v, cost));
graph.get(v).add(new Edge(u, cost));
}
st = new StringTokenizer(br.readLine());
v1 = Integer.parseInt(st.nextToken());
v2 = Integer.parseInt(st.nextToken());
solutions();
}
static void solutions() {
// 1 -> v1 -> v2 -> N으로 가는 경우
int res1 = 0;
res1 += dijkstra(1, v1);
res1 += dijkstra(v1, v2);
res1 += dijkstra(v2, N);
// 1 -> v2 -> v1 -> N으로 가는 경우
int res2 = 0;
res2 += dijkstra(1, v2);
res2 += dijkstra(v2, v1);
res2 += dijkstra(v1, N);
int ans = (res1 >= INF && res2 >= INF) ? -1 : Math.min(res1, res2);
System.out.println(ans);
}
public static int dijkstra(int start, int end) {
Arrays.fill(dist, INF);
Arrays.fill(check, false);
PriorityQueue<Edge> pq = new PriorityQueue<>();
boolean[] check = new boolean[N + 1];
pq.offer(new Edge(start, 0));
dist[start] = 0;
while (!pq.isEmpty()) {
Edge curEdge = pq.poll();
int cur = curEdge.u;
if (!check[cur]) {
check[cur] = true;
for (Edge edge : graph.get(cur)) {
if (!check[edge.u] && dist[edge.u] > dist[cur] + edge.cost) {
dist[edge.u] = dist[cur] + edge.cost;
pq.add(new Edge(edge.u, dist[edge.u]));
}
}
}
}
return dist[end];
}
}
'알고리즘' 카테고리의 다른 글
| [알고리즘, BOJ] 11066 파일 합치기 - java (1) | 2025.06.16 |
|---|---|
| 알고리즘에서 이벤트 기반 접근 (5) | 2024.11.11 |
| [알고리즘, BOJ] 1109 섬 - java (3) | 2024.10.19 |
| [알고리즘, BOJ] 17071 숨바꼭질 5 - java (2) | 2024.10.17 |
| [알고리즘, 코드트리] 왕실의 기사 대결 - java (4) | 2024.10.11 |


댓글