
문제
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 500,000)에 있고, 동생은 점 K(0 ≤ K ≤ 500,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다. 동생은 항상 걷기만 한다. 동생은 항상 매 초마다 이동을 하며, 이동은 가속이 붙는다. 동생이 이동하는 거리는 이전에 이동한 거리보다 1을 더한 만큼 이동한다. 즉, 동생의 처음 위치는 K, 1초가 지난 후 위치는 K+1, 2초가 지난 후 위치는 K+1+2, 3초가 지난 후의 위치는 K+1+2+3이다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오. 동생을 찾는 위치는 정수 좌표이어야 하고, 수빈이가 0보다 작은 좌표로, 50만보다 큰 좌표로 이동하는 것은 불가능하다.
입력
첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.

출력
수빈이가 동생을 찾는 가장 빠른 시간을 출력한다. 수빈이가 동생을 찾을 수 없거나, 찾는 위치가 500,000을 넘는 경우에는 -1을 출력한다.

문제 풀이
숨바꼭질은 정말 유명한 문제로 bfs를 활용하는 것으로 잘 알려진 유형이다. 이번에도 bfs 응용으로 문제를 접근해보자. 기존의 숨바꼭질 문제와 다른 점은 동생"도" 함께 움직인다는 점이다. 동생은 하나의 방향으로 등가속도 직선 운동을 한다. 수빈이는 움직이는 동생을 따라잡거나 기다려야 한다.
잠깐만 기다린다고?

예제 입력 2를 살펴보자.

동생의 시간에 따른 움직임을 살펴보면 아래와 같이 움직인다.

이 때, 수빈이의 움직임을 함께 고려해보자.
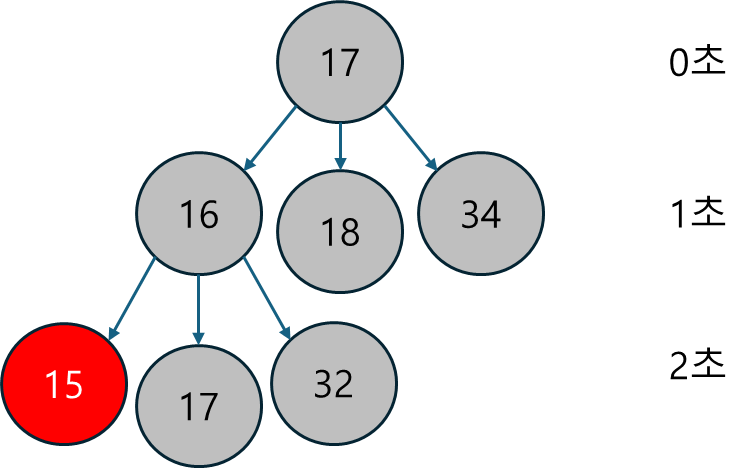
동생이 출발한 지 4초 후에 도착할 위치 15를 수빈이는 2초 만에 갈 수 있다. 즉, 수빈이가 15위치에서 한번 왔다갔다 하면 4초에 15에서 만나는 경우가 최단시간 만에 만나는 경우가 된다. 더 쉽게 시간에 따른 두 사람의 위치를 그림으로 살펴보자.

2초에 수빈이 15에 도달했다. 동생이 4초에 15에 도착하는 걸 미리 알았다면 아래와 같이 움직일 것이다.

둘 다 움직이고 있기 때문에 이처럼 왔다갔다 하는 의미없는 움직임을 통해서 두 사람이 만나는 최단 시간이 변화할 수 있다. 단, 이런 경우가 되기 위해서는 동생이 "짝수 턴"에 도착할 위치에 수빈도 "짝수 턴"에 도달해야 한다는 점이 중요하다. 왔다갔다 두 개의 턴이 소모되므로 반드시 홀수, 짝수 턴을 체크해야 한다.
자 이제 코드를 작성해보자.
자료구조 정의 및 입출력
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
if(N == K) {
System.out.println(0);
return;
}
int[] map = new int[500001];
boolean[][] visit = new boolean[2][500001];
Arrays.fill(map, -1);
int dist = 0;
int cnt = 0;
while (K + dist <= 500000) {
K += dist;
dist++;
map[K] = cnt++;
bro.add(K);
}동생이 어느 위치에 몇 턴에 도달하는지 기록하기 위해 map 배열을 인풋사이즈의 최대 크기(500000)만큼 선언해 준다. 또, 수빈이는 특정 위치에 짝수 턴에 도달하게 될지, 홀수 턴에 도달하게 될지를 체크해야 하기 때문에 방문 배열 visit는 2차원 배열로 선언하였다.
그 후, map배열을 조건에 맞게 초기화해준다. map 배열의 인덱스는 위치를 의미하고 map [i]의 값이 -1이라면 i 위치에 도달하지 못함을, map[i] > k > 0이라면 i 위치에 k 턴에 도달한다는 의미이다.
bfs 응용
Queue<int[]> q = new ArrayDeque<>();
// 현재 위치 N, 현재 시간 0
int[] now = new int[]{N, 0};
q.add(now);
int min_time = Integer.MAX_VALUE;
a:while (!q.isEmpty()) {
now = q.poll();
for (int next : new int[]{now[0] + 1, now[0] - 1, now[0] * 2}) {
int nextTime = now[1] + 1;
if (next > 500000 || next < 0) {
continue;
}
if(visit[nextTime % 2][next]) {
if(nextTime % 2 == map[next] % 2 && map[next] >= nextTime) {
min_time = Math.min(min_time, map[next]);
}
continue;
}
if (map[next] == nextTime) {
min_time = Math.min(min_time, nextTime);
break a;
}
q.add(new int[]{next, nextTime});
visit[nextTime % 2][next] = true;
}
}bfs에 사용할 queue에는 int []를 저장할 것이다. 첫 번째 인덱스에는 위치를, 두 번째 인덱스에는 턴을 저장한다.
함께 도달할 수 있는 최소의 시간대를 구하기 위해 min_time이라는 정답에 활용할 변수도 선언하자.
여느 때와 다름없는 bfs를 수행할 거지만 조건 설정이 조금 까다롭다.
다음 위치 next가 다음 턴(짝수 턴 or 홀수 턴) nextTime % 2에 이미 방문되어 있다면 이 뒤로 있을 경우의 수는 보지 않아도 되기 때문에 queue에 넣지 않을 것이다. 단, 이 경우 뒷 턴에 동생이 next 위치를 방문하는 경우라면 답이 될 자격이 있으므로 min_time을 계산해준다.
if(visit[nextTime % 2][next]) {
if(nextTime % 2 == map[next] % 2 && map[next] >= nextTime) {
min_time = Math.min(min_time, map[next]);
}
continue;
}
이렇게 복잡하게 생각할 필요 없이 만약 처음 map [next]가 nextTime을 만나는 때가 온다면 bfs특성상 무조건 최단 시간이므로 min_time을 계산해준다.
if (map[next] == nextTime) {
min_time = Math.min(min_time, nextTime);
break a;
}전체 코드
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
if(N == K) {
System.out.println(0);
return;
}
int[] map = new int[500001];
boolean[][] visit = new boolean[2][500001];
Arrays.fill(map, -1);
ArrayList<Integer> bro = new ArrayList<>();
int dist = 0;
int cnt = 0;
while (K + dist <= 500000) {
K += dist;
dist++;
map[K] = cnt++;
bro.add(K);
}
Queue<int[]> q = new ArrayDeque<>();
// 현재 위치 N, 현재 시간 0
int[] now = new int[]{N, 0};
q.add(now);
int min_time = Integer.MAX_VALUE;
a:while (!q.isEmpty()) {
now = q.poll();
for (int next : new int[]{now[0] + 1, now[0] - 1, now[0] * 2}) {
int nextTime = now[1] + 1;
if (next > 500000 || next < 0) {
continue;
}
if(visit[nextTime % 2][next]) {
if(nextTime % 2 == map[next] % 2 && map[next] >= nextTime) {
min_time = Math.min(min_time, map[next]);
}
continue;
}
if (map[next] == nextTime) {
min_time = Math.min(min_time, nextTime);
break a;
}
q.add(new int[]{next, nextTime});
visit[nextTime % 2][next] = true;
}
}
System.out.println(min_time == Integer.MAX_VALUE ? -1 : min_time);
}
}문제 풀이 소요 시간 : 1시간 30분
'알고리즘' 카테고리의 다른 글
| 알고리즘에서 이벤트 기반 접근 (5) | 2024.11.11 |
|---|---|
| [알고리즘, BOJ] 1109 섬 - java (3) | 2024.10.19 |
| [알고리즘, 코드트리] 왕실의 기사 대결 - java (4) | 2024.10.11 |
| [알고리즘, 코드트리] 코드트리 메신저 - java (1) | 2024.10.11 |
| [알고리즘, 코드트리] 루돌프의 반란 - java (4) | 2024.10.10 |


댓글